개요
연속적인 시계열 데이터를 살펴보면서 간혹 급격하게 수치가 상승, 혹은 하강하는 경우가 있다.
마치 비트코인의 시장가격 처럼.
이런 경우 더 최악의 상황이 되기 전에 올바른 방향으로 제어를 할 필요가 있다.
CPD(Change Point Detection, 변화 지점 탐지) 기술을 활용을 통해 데이터의 이상치 발생을 파악하여 급격한 Trend의 변화가 있다면 이를 감지하도록 한다.
예시를 들면 그날 하루 폭염주의보가 발령이 된다고 했을때,
평상시와는 다른 급격하게 온도 변화를 보이는 구간을 파악하여 해당 시점을 기준으로 폭염주의보를 발령하는 것이다.
이러한 CPD 기술을 바탕으로 데이터 변화점 탐지를 진행할 예정 이다.
알고리즘 선정
일단 CPD에서 사용할수 있는 다양한 방법들이 있는 것을 알수 있다.
한번 GPT에게 물어보자
현대 기술력의 위대함을 목도하라

자 일단 딱봐도 1. CUSUM, 2. EWMA가 만만해보인다.
사실 3. PELT 알고리즘을 써서 해보았는데 뭔가 잘 안된다.
일단 PELT 알고리즘의 코드 부터 적어 보겠다. 누군가는 잘 쓰겠지
PELT(Pruned Exact Linear Time)
시계열 데이터에서 변화 지점을 탐지하는 기법중 하나
python에서 ruptures 라이브러리를 통해서 구현 가능함
pen(패널티)수치를 도입해서 변화점 수에 대한 패널티를 부여서 과적합을 방지 가능
(1이상의 양의 정수를 사용, 커질수록 검출이 유해진다. 1이면 깐깐하게 검출하고)
import ruptures as rpt
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 해당 기간의 분단위 시간, 기온 데이터를 가져온다. (1440개 = 24시간 * 60분)
d=bring_aircon("2019-08-02 00:00:00", "2019-08-03 00:00:00")
signal = [_['temp'] for _ in d]
time = [_['time'] for _ in d]
signal = np.array(signal)
time = np.array(time)
# Pelt 알고리즘을 사용하여 change point detection
model = rpt.Pelt(model="l1").fit(signal)
print(len(signal))
# 패널티값을 1부터 9까지의 정수를 넣어가면서 비교함
for i in range(1,10):
result = model.predict(pen=i)
print(result)
# 결과 시각화
plt.figure(figsize=(25, 9))
plt.plot(signal, label='Original Signal')
for change_point in result:
plt.axvline(x=change_point, color='red', linestyle='--', label='Change Point')
plt.savefig(f'asd{i}.png')
bring_aircon()함수는 내가 임의로 만든 함수 이다. 데이터는 원하는 대로 바꾸면 된다.
이제 맷플롯립을 통해서 만들어진 이미지를 함께 살펴보자
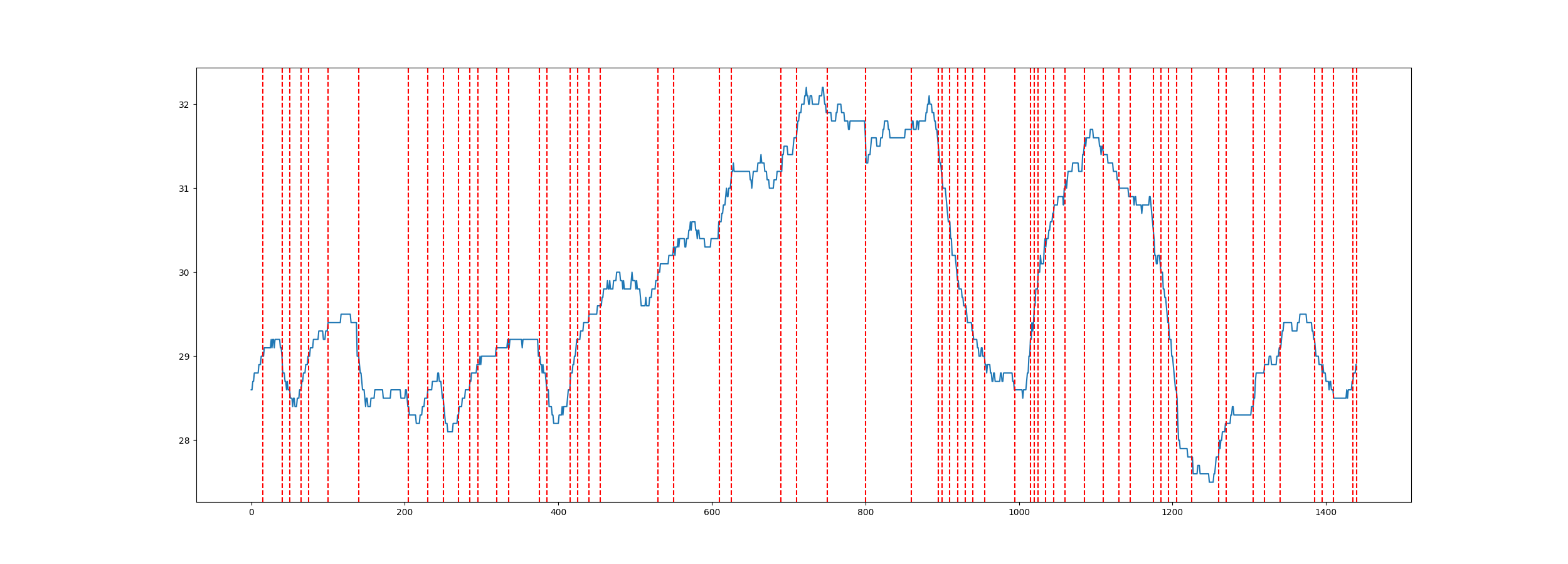

패널티를 작게 준쪽이 좀더 세밀하게 검출하는것을 볼수 있고, 패널티를 크게 준쪽이 보다 여유있게 검출을 하는것을 볼수 있다. 패널티값을 어떻게 설정하는가가 핵심이라고 볼수 있다.
근데 아쉽게도 생각보다 잘 안된다. 아래 그림을 보자 하늘색 선이 누가봐도 에어컨을 켜고 끈 시간이다. 내가 원하는건 에어컨을 언제 키고 껏는지를 의미하는 시각인데, PELT 가 잘 검증하지 못한다. 따라서 1,2번 방법을 한번 실행 해보고, 그래도 안되는 것이면 3번 PELT 방법을 활용해서 어떻게 해야 할지 고민을 좀 해봐야 겠다.
CUSUM(cumulative sum)
누적 합계를 이용하여 특정 양 만큼 쌓이다 넘치는 순간?
어 더이상 못담아 뒤에 값을 이상치야~ 하는 원리 이다.
아쉽게도 내가 원하는 에어컨 작동 시점과는 어울리지 않다. 누적 방식은 뭐 자원 생산 같은거에 쓸수는 있겠는데, 내가 원하는 방시식은 이게 아니다. 아쉽지만 Pass

이거는 아무래도 누적합 방식이다보니, 안될것 같다... 나는 특정 구간에서 급격한 변화가 발생하면 그때를 캐치하고 싶은건데 말이야
코드는 아래와 같다
import numpy as np
import matplotlib.pyplot as plt
def cusum(data, threshold=5):
n = len(data)
mean_value = np.mean(data)
cusum_values = np.zeros(n)
exceed_threshold = []
for i in range(1, n):
cusum_values[i] = max(0, cusum_values[i-1] + data[i] - mean_value)
if cusum_values[i] > threshold:
exceed_threshold.append(i)
return cusum_values, exceed_threshold
# 가상의 시계열 데이터 생성
np.random.seed(42)
time_points = np.arange(100)
signal = np.concatenate([np.random.normal(0, 1, 50), np.random.normal(5, 1, 50)])
# CUSUM 알고리즘 적용
cusum_values, change_points = cusum(signal)
# 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(time_points, signal, label='Original Signal')
plt.plot(time_points, cusum_values, label='CUSUM Values', linestyle='--', color='red')
plt.scatter(change_points, signal[change_points], color='red', label='Change Points')
plt.legend()
plt.savefig('cusum.png')
EWMA(Exponentially Weighted Moving Average)
지수가중이동평균을 측정하여 cpd 지점을 탐지 한다.
지수가중이동평균이란,
지수는 여러분들이 아는 2^x승 이런거 맞다.
가중은 가중치를 의미한다.
이동이란 슬라이딩 윈도우 방식이라고 해서, 유리창을 수건으로 닦듯, 특정 영역의 크기만큼 점점 데이터를 타고 이동하면서 보는 방식 이다.
위의 3 단어를 합쳐보면, 특정 영역의 데이터의 평균을 구하되, 최근값에 해당하는 부분에 지수승의 가중치를 주어서, 최신 데이터 트렌드를 더 많이 반영하면서 해당 영역의 트렌드를 반영하는 것이다. 이 때 구간별 측정한 영역의 가중평균을 비교하면서 갑자기 변함을 감지하면? CPD로 추측할수 있는것이다.
무슨말이냐? 아래의 그림을 보라
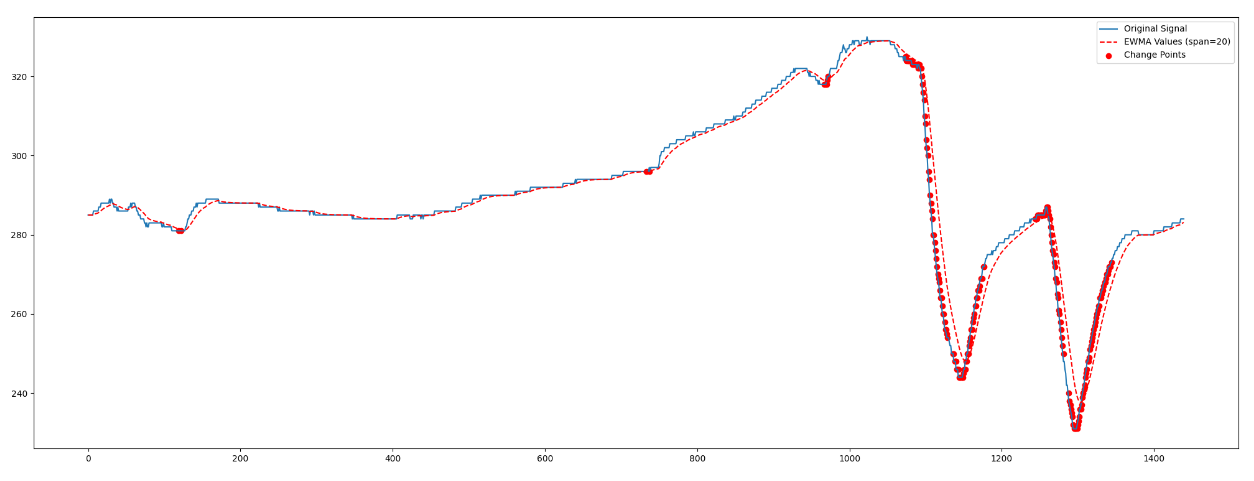
위의 그림은 특정 영역의 8월 여름 하루 동안의 온도변화 그래프 이다. (X축이 0~1440인 이유: 24시간 * 60분 = 1440분)
Y축은 온도*10한 값이다.(30.2도면 302로 표기 됨, 이유: 저 점을 찍는 matplotlib scatter 함수가 정수값에만 쓸수 있기 때문)
저는 여기서 span값(탐지하는영역 크기)를 20분으로 설정하고, CPD라고 판단하는 기준은 영역별 차이가 0.3도가 되는 순간 이상치(뭔가 사용자가 했구나? 에어컨 켜기 같이)로 판단하기로 하였다.(threshhold = 3 이라고 설정 함)
참고로 span과 Treshhold는 내가 직접 1~50 까지 직접 변경해가면서 찾은 값이다.(데이터별 파라미터 조절이 까다로움으로, 이렇게 잘 해야 한다는 말이다)
위의 점을 잘 보면 꽤 잘 되는것 같다? 실제 에어콘 On off 영역도 거의 일치 하는것으로 보인다.
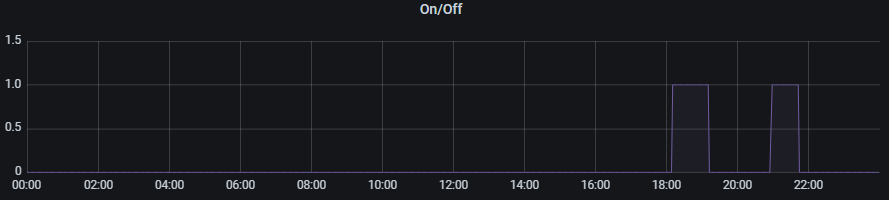
나름 만족스러운 부분 이다.
코드는 아래와 같다
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import datetime
# 5분 간격으로 진행 한다.
def ewma_cpd(data, span, threshold=3):
"""
Exponential Weighted Moving Average (EWMA) Change Point Detection.
Parameters:
- data: 시계열 데이터
- span: 이동 평균의 스팬 값
- threshold: 변화점으로 감지할 임계값
Returns:
- ewma_values: EWMA 적용 결과
- change_points: 변화점의 인덱스 리스트
"""
ewma_values = data.ewm(span=span, adjust=False).mean()
delta = np.abs(data - ewma_values)
change_points = np.where(delta > threshold)
return ewma_values, change_points
date1 = "2019-08-21 00:00:00"
date2 = "2019-08-22 00:00:00"
d = bring_aircon(date1, date2)
signal = [int(_['temp']*10) for _ in d] # 온도 정보를 담고 있음 (실수)
#time = [_['time'] for _ in d] # 시간값
# 가상의 시계열 데이터 생성
time_points = np.arange(len(signal)) # 0부터 1339까지의 숫자가 담긴 배열이 생성 된다.
# EWMA 알고리즘 적용
span_value = 20 # 이동 평균의 스팬 값(분)
ewma_values, change_points = ewma_cpd(pd.Series(signal), span=span_value, threshold=2)
print(np.array(change_points[0])-span_value)
뭇 = [signal[i-1] for i in np.array(change_points[0])-span_value]
# 결과 시각화
plt.figure(figsize=(25, 9))
plt.plot(time_points, signal, label='Original Signal')
plt.plot(time_points, ewma_values, label=f'EWMA Values (span={span_value})', linestyle='--', color='red')
#plt.scatter(change_points,뭇, color='red', label='Change Points')
plt.scatter(np.array(change_points[0])-span_value,뭇, color='red', label='Change Points')
plt.legend()
plt.savefig(f'{date1}ewma_cpd_span20_thrshol3.png')
데이터가 가져 오는건 분단위의 온도값이라고 생각하면 된다.
CPD, MPC 세미나 진행후 피드백 -----------------------------------------
연구소에서 CPD 세미나를 진행한뒤 다양한 피드백을 받았습니다. 제가 그린 그래프는 스무딩 해서 점을 찍은것 같다고, 살짝 핀트가 어긋난것 같다는 피드백을 받았습니다. 그냥 단순하게 미분해서 해보는 방법을 시도해보도록 하였습니다.
또한 CPD를 직접 구현하기보다는, 논문과 GIthub에 코드가 있으니 참고해서 다시 구현해보라고 하셨습니다.
Paperswithcode라는 논문사이트에서 CPD를 검색해보니 다양한 구현방법과 소개논문이 존재하는걸 확인했습니다.
https://paperswithcode.com/task/change-point-detection
Papers with Code - Change Point Detection
**Change Point Detection** is concerned with the accurate detection of abrupt and significant changes in the behavior of a time series. Change point detection is the task of finding changes in the underlying model of a signal or time series. They are two m
paperswithcode.com
그중에서 저는 베이지안 CPD 방법을 한번 활용해보려고 합니다. 아래 코드를 바탕으로 데이터만 제가 사용하는 것으로 바꾸어서 활용할 예정 입니다. 잘 되길 바랍니다...
GitHub - hildensia/bayesian_changepoint_detection: Methods to get the probability of a changepoint in a time series.
Methods to get the probability of a changepoint in a time series. - GitHub - hildensia/bayesian_changepoint_detection: Methods to get the probability of a changepoint in a time series.
github.com
제가 발표준비한 PPT는 아래에 첨부합니다.
'알아두면좋은IT상식' 카테고리의 다른 글
| GPU 활용한 텐서플로 가동(결국 실패함) (0) | 2024.03.31 |
|---|---|
| [논문 분석] 강우자료의 비동질성 규명을 위한 변동점 분석기법의 상호비교 및 적용 (1) | 2024.01.10 |
| [CS] 디자인 패턴과 프로그래밍 패러다임 part 1 (2) | 2023.10.26 |
| [머신러닝/딥러닝] 자주 등장하는 용어 정리 (0) | 2023.07.20 |
| [Git&Github] 깃이란 무엇인가 그리고 깃허브는 어떻게 쓰는건가? part 2 (0) | 2023.07.07 |


